Design > DOE > Design of Experiments (DOE)
Design of Experiments
Example
Suppose we want to test alternative movie theater designs using three factors.
- Price at $10, $13, or $16
- Sight to determine if theater setting should be staggered or not staggered
- Food to determine if we should offer hot dogs and popcorn, gourmet food, or no food at all
Max levels
The factors to include in the analysis have 3, 2, and 3 levels so we enter 3 in the Max levels input.
Variable name, Level 1, Level 2, and Level 3
Here we will enter the factors of interest. For example, enter price as the variable name, $10 as level 1, $13, as level 2, and $16 as level 3. Then click the icon. This will enter the specification details required into the Design factors window in the format Radiant needs for the analysis. To remove a line click the icon.
After entering the required information your screen should look as follows:
Create
You are now ready to create an experimental design by clicking on the Create button. This will generate the following output.
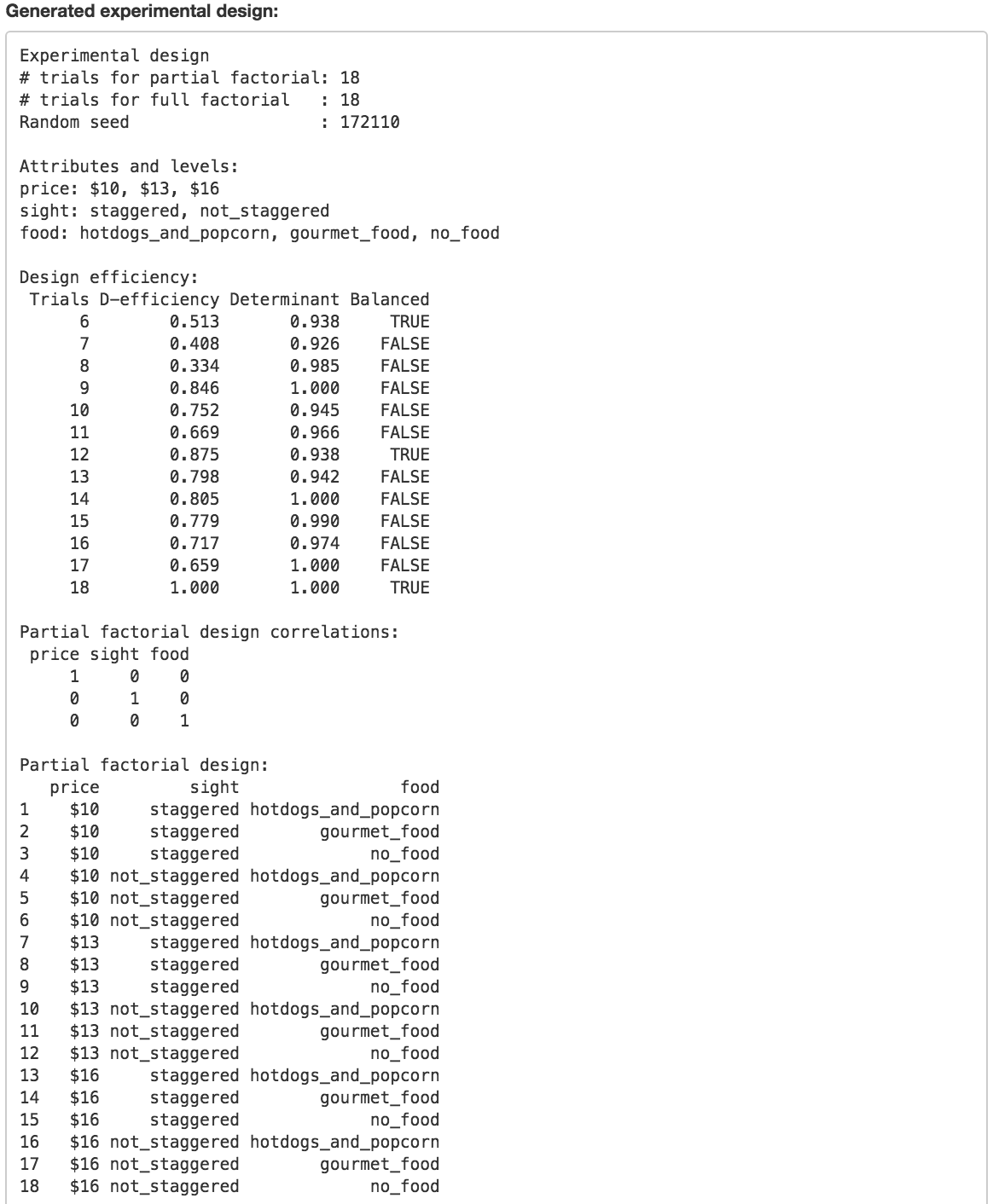
For our example, the ideal design has 18 trials. However, this implies that the partial and the full factorial are the same size. We’d like to find out if it is possible to reduce the number of trials. See # trials below.
# trials
This input can be used to control the number of trials to generate. If left blank Radiant will try to find an appropriate number of trials using the optFederov routine in R.
Lets review the output in Design efficiency. The goal is to find a design with less than 18 trials that will still allow us to estimate the effects we are interested in (e.g., the main-effects of the different levels of price, sight, and food). Notice that there are several designs that are considered balanced (i.e., each level is included in the same number of trials). We are looking for a design that is (1) balanced, (2) has minimal correlation between factors (i.e., a determinant close to 1), and (3) that has a D-efficiency score above .8. You can think of the D-efficiency score as a measure of how easily we will be able to estimate the effects of interest after running the test/experiment. Again, the ideal D-efficiency score is 1 but a number above .8 is quite reasonable.
The smallest number of trials with a balanced design is 6. This design is balanced simply because 6 is divisible by 3 and 2 (i.e., the number of levels in our factors). However, although the design has a Determinant close to 1, the D-efficiency score is rather low (.513). The next smallest balanced design has 12 trials and a high value for both the Determinant and D-efficiency. This design is appropriate if we want to be able to estimate the main-effects of each factor level on movie-theater choice or preference.
Rnd. seed:
A partial factorial design need not be unique (i.e., there might be multiple combinations of trials or profiles that are equally good). By setting a random seed you ensure you will get the same set of trials each time you press Create. However, to see if there are other options, empty the Rnd. seed box and press Create a few times.
Interactions
Note that we will not be able to estimate all possible interactions between price, sight, and food if we use a design with 12 trials. This is the trade-off inherent in partial factorial designs! In fact, if we do want to estimate even one interaction (e.g., select price:sight) the appropriate design has 18 trials (i.e., the number in the full factorial design that includes all possible combinations of factor levels).
Create, Partial, Full
These buttons can be used to Create the full and partial factorial designs. To download the design you want in csv format click on the either the Partial or the Full button.
Upload and Download
You can download the list of factors you entered by clicking the Download button. To upload a previously entered set of factors click the Upload button.
